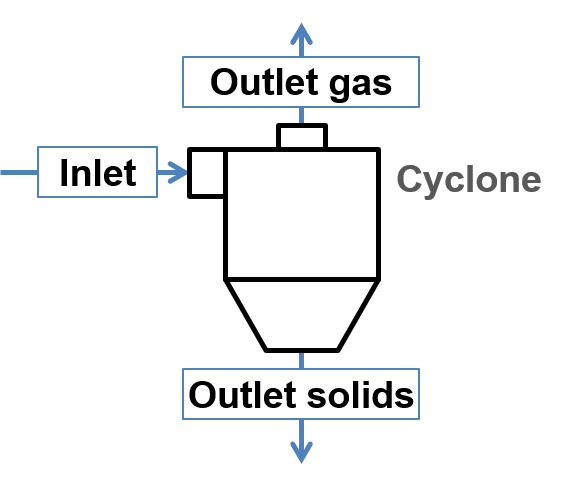
Cyclone

Solids-gas separation according to Muschelknautz

Constant geometric parameters

$r_{o} = 0.5d_{o}$

$r_{f} = 0.5d_{f}$

$r_{exit} = 0.5d_{exit}$

$b_{e} = \begin{cases} \text{user-defined} & \text{rect slot, full/half spiral entry} \\ r_{o} - r_{core} & \text{axial entry} \end{cases}$

$r_{e} = \begin{cases} r_{o} - 0.5b_{e} & \text{rect slot, axial entry} \\ r_{o} + 0.5b_{e} & \text{full spiral entry} \\ r_{o} & \text{half spiral entry} \\ \end{cases}$

${\overline{r}}_{con} = 0.5\left( r_{o} + r_{exit} \right)$

$r_{exit,eff} = \begin{cases} r_{f} & r_{exit} \leq r_{f} \\ r_{exit} & r_{exit} > r_{f} \\ \end{cases}$

$\beta = \frac{b_{e}}{r_{o}}$

$h_{con} = h_{tot} - h_{cyl}$

$h_{con,eff} = \left( \frac{r_{o} - r_{exit,eff}}{r_{o} - r_{exit}} \right)h_{con}$

$h_{sep} = h_{cyl} + h_{con,eff} - h_{f}$

$a = \begin{cases} \text{-} & \text{rect slot, full/half spiral entry} \\ \sin(\delta)\frac{\pi\left( r_{o} + r_{core} \right)}{N_{b}} - d_{b} & \text{axial entry} \\ \end{cases}$

$A_{cyl} = 2\pi r_{o}h_{cyl}$

$A_{con} = \pi\left( r_{o} + r_{exit,eff} \right)\sqrt{h_{con,eff}^{2} + \left( r_{o} - r_{exit,eff} \right)^{2}}$

$A_{top} = \pi r_{o}^{2} - \pi r_{f}^{2}$

$A_{f} = 2\pi r_{f}h_{f}$

$A_{tot} = \begin{cases} A_{cyl} + A_{con} + A_{f} + A_{top} & \text{rect slot, axial entry} \\ A_{cyl} + A_{con} + A_{f} + A_{top} - \varepsilon r_{o}h_{e} & \text{full/half spiral entry} \\ \end{cases}$

$A_{con/2} = \pi\left( r_{o} + {\overline{r}}_{con} \right)\sqrt{\left( \frac{h_{con}}{2} \right)^{2} + \left( r_{o} - {\overline{r}}_{con} \right)^{2}}$

$A_{sed} = A_{cyl} + A_{con/2}$

$A_{e1} = \frac{2\pi r_{o}h_{e}}{2}$

$A_{sp} = \begin{cases} \text{-} & \text{rect slot, axial entry} \\ \varepsilon\left( \frac{b + 2r_{o}}{2}\left( b_{e} + h_{e} \right) \right) & \text{full spiral entry} \\ \varepsilon r_{o}\left( b_{e} + h_{e} \right) & \text{half spiral entry} \\ \end{cases}$

Operational parameters

${\dot{V}}_{in,g} = \frac{{\dot{m}}_{in,g}}{\rho_{g}}$

$\mu_{in} = \frac{{\dot{m}}_{in,s}}{{\dot{m}}_{in,g}}$

$\lambda_{s} = \begin{cases} \lambda_{0}\left( 1 + 2\sqrt{\mu_{in}} \right) & \mu_{in} \leq 1 \\ \lambda_{0}\left( 1 + 3\sqrt{\mu_{in}} \right) & \mu_{in} > 1 \\ \end{cases}$

$\alpha = \begin{cases} \frac{1}{\beta}\left( 1 - \sqrt{1 + 4\left\lbrack \left( \frac{\beta}{2} \right)^{2} - \left( \frac{\beta}{2} \right) \right\rbrack\sqrt{1 - \frac{1 - \beta^{2}}{1 + \mu_{in}}\left( 2\beta - \beta^{2} \right)}} \right) & \text{rect slot, full/half spiral entry} \\ \begin{cases} 0.85 & \text{simple straight blades} \\ 0.95 & \text{curved blades} \\ 1.05 & \text{curved and twisted blades} \\ \end{cases} & \text{axial entry} \\ \end{cases}$

Geometric parameters

${\overline{r}}_{e} = r_{o} - \frac{\alpha b_{e}}{2}$

${\overline{r}}_{z} = \sqrt{{\overline{r}}_{e}{\overline{r}}_{con}}$

Velocities

$v_{e} = \begin{cases} {\dot{V}}_{in,g}/\left( b_{e}h_{e} \right) & \text{rect slot, full/half spiral entry} \\ {\dot{V}}_{in,g}/\left( ab_{e}N_{b} \right) & \text{axial entry} \\ \end{cases}$

$w_{50} = \frac{0.5\left( 0.9{\dot{V}}_{in,g} \right)}{A_{sed}}$

$u_{o} = \begin{cases} \frac{v_{e}\frac{r_{e}}{r_{o}}}{\alpha} & \text{rect slot entry} \\ \frac{v_{e}\frac{r_{e}}{r_{o}}}{1 + \frac{\lambda_{s}}{2}\frac{A_{sp}}{{\dot{V}}_{in,g}}v_{e}\sqrt{\frac{r_{e}}{r_{o}}}\ } & \text{full/half spiral entry} \\ \frac{v_{e}\cos(\delta)\frac{r_{e}}{r_{o}}}{\alpha} & \text{axial entry} \\ \end{cases}$

$u_{f} = \frac{u_{o}\frac{r_{o}}{r_{f}}}{1 + \frac{\lambda_{s}}{2}\frac{A_{tot}}{{\dot{V}}_{in,g}}u_{o}\sqrt{\frac{r_{o}}{r_{f}}}}$

$u_{e} = \frac{u_{o}\frac{r_{o}}{{\overline{r}}_{e}}\ }{1 + \frac{\lambda_{s}}{2}\frac{A_{e1}}{0.9{\dot{V}}_{in,g}}u_{o}\sqrt{\frac{r_{o}}{{\overline{r}}_{e}}}}$

$u_{con} = \frac{u_{o}\frac{r_{o}}{{\overline{r}}_{con}}\ }{1 + \frac{\lambda_{s}}{2}\frac{A_{sed}}{0.9{\dot{V}}_{in,g}}u_{o}\sqrt{\frac{r_{o}}{{\overline{r}}_{con}}}}$

Mass separation between main and secondary streams

$n = \frac{\ln\frac{u_{f}}{u_{o}}}{\ln\frac{r_{o}}{r_{f}\ }}$

${\dot{V}}_{\sec} = {\dot{V}}_{in,g}\left( 0.0497 + 0.0684n + 0.0949n^{2} \right)$

$w_{split} = 1 - \frac{{\dot{V}}_{\sec}}{{\dot{V}}_{in,g}}$

Separation at wall due to exceeding the loading limit in main stream

${\overline{z}}_{e} = \frac{u_{e}u_{con}}{{\overline{r}}_{z}}$

$d_{main,l}^{*} = \sqrt{w_{50}\frac{18\eta_{visc}}{\left( \rho_{s} - \rho_{g} \right){\overline{z}}_{e}}}$

$k = \begin{cases} 0.81 & \mu_{in} < 2.2 \cdot 10^{- 5} \\ 0.15 + 0.66\exp\left( - \left( \frac{\mu_{in} - 2.2 \cdot 10^{- 5}}{0.015 - 2.2 \cdot 10^{- 5}} \right)^{0.6} \right) & 2.2 \cdot 10^{- 5} \leq \mu_{in} < 0.015 \\ 0.15 + 0.66\exp\left( - \left( \frac{0.1 - 0.015}{0.1 - \mu_{in}} \right)^{0.1}\left( \frac{\mu_{in}}{0.015} \right)^{0.6} \right) & 0.015 \leq \mu_{in} \leq 0.1 \\ 0.15 & \mu_{in} > 0.1 \\ \end{cases}$

$\mu_{main} = K_{main}\left( \frac{d_{main,l}^{*}}{d_{50}} \right)\left( 10\mu_{in} \right)^{k}$

$\eta_{main,l} = 1 - \frac{\mu_{main}}{\mu_{in}}$

Separation in the internal vortex of main stream

$d_{main,v}^{*} = \sqrt{\frac{18\eta_{visc}0.9{\dot{V}}_{in,g}}{\left( \rho_{s} - \rho_{g} \right)u_{f}^{2}2\pi h_{sep}}}$

$\eta_{main,v}(d) = \begin{cases} 0 & \frac{d}{d_{main,v}^{*}} < D^{- 1} \\ 0.5\left\{ 1 + \cos\left\lbrack 0.5\pi\left( 1 - \frac{\log\left( \frac{d}{d_{main,v}^{*}} \right)}{\log D} \right) \right\rbrack\ \right\} & D^{- 1} \leq \frac{d}{d_{main,v}^{*}} \leq D \\ 1 & \frac{d}{d_{main,v}^{*}} > D \\ \end{cases}$

Separation at wall due to exceeding the loading limit in secondary stream

$\mu_{\sec} = \begin{cases} 6\mu_{main} & \mu_{in} \geq 6\mu_{main} \\ \mu_{in} & \mu_{in} < 6\mu_{main} \\ \end{cases}$

$\eta_{sec,l} = 1 - \frac{\mu_{\sec}}{\mu_{in}}$

Separation at vortex finder of secondary stream

$d_{sec,v}^{*} = \sqrt{\frac{18\eta_{visc}{\dot{V}}_{\sec}}{\left( \rho_{s} - \rho_{g} \right)\left( \frac{2}{3}u_{f} \right)^{2}2\pi h_{f}}}$

$\eta_{sec,v}(d) = \begin{cases} 0 & \frac{d}{d_{sec,v}^{*}} < D^{- 1} \\ 0.5\left\{ 1 + \cos\left\lbrack 0.5\pi\left( 1 - \frac{\log\left( \frac{d}{d_{sec,v}^{*}} \right)}{\log D} \right) \right\rbrack\ \right\} & D^{- 1} \leq \frac{d}{d_{sec,v}^{*}} \leq D \\ 1 & \frac{d}{d_{sec,v}^{*}} > D \\ \end{cases}, \text{with } D = 3$

Overall separation

$\eta_{main}(d) = \begin{cases} \eta_{main,l} + \left( 1 - \eta_{main,l} \right)\eta_{main,v}(d) & \mu_{in} > \mu_{main} \\ \eta_{main,v}(d) & \mu_{in} \leq \mu_{main} \\ \end{cases}$

$\eta_{\sec}(d) = \begin{cases} \eta_{sec,l} + \left( 1 - \eta_{sec,l} \right)\eta_{sec,v}(d) & \mu_{in} > \mu_{\sec} \\ \eta_{sec,v}(d) & \mu_{in} \leq \mu_{\sec} \\ \end{cases}$

$\eta_{tot}(d) = \eta_{adj}\left( w_{split}\eta_{main}(d) + \left( 1 - w_{split} \right)\eta_{\sec}(d) \right)$

${\dot{m}}_{s,out,s} = {\dot{m}}_{in,s}\sum_{d}^{}{R_{in}(d)\eta_{tot}(d)}$

${\dot{m}}_{s,out,g} = 0$

${\dot{m}}_{g,out,s} = {\dot{m}}_{in,s}\left( 1 - \sum_{d}^{}{R_{in}(d)\eta_{tot}(d)} \right)$

${\dot{m}}_{g,out,g} = {\dot{m}}_{in,g}$

Note

Notations:

Symbol	Units	Type	Description
$\beta$	[-]		Relative width of cyclone gas entry
$\delta$	[°]	UP	Angle of attack of blades in axial gas entry
$\varepsilon$	[°]	UP	Spiral angle in spiral gas entry
$\lambda_{0}$	[-]	UP	Wall friction coefficient of pure gas
$\lambda_{s}$	[-]		Wall friction coefficient of solids-containing gas
$\mu_{in}$	[kg/kg]		Solids loading at inlet
$\mu_{main}$	[kg/kg]		Threshold for solids loading in main stream
$\mu_{\sec}$	[kg/kg]		Threshold for solids loading in secondary stream
$\eta_{adj}$	[-]	UP	Separation efficiency adjustment factor
$\eta_{main}$	[-]		Overall separation efficiency in main stream
$\eta_{main,l}$	[-]		Separation efficiency due to exceeding of solids loading limit in main stream (from main stream to solids output)
$\eta_{main,v}$	[-]		Separation efficiency in internal vortex (from internal vortex to solids output)
$\eta_{\sec}$	[-]		Overall separation efficiency in secondary stream
$\eta_{sec,l}$	[-]		Separation efficiency due to exceeding of solids loading limit in secondary stream (from secondary stream to solids output)
$\eta_{sec,v}$	[-]		Separation efficiency at vortex finder (from vortex finder to solids output)
$\eta_{tot}$	[-]		Total separation efficiency of cyclone
$\eta_{visc}$	[Pa s]	MDB	Dynamic viscosity of gas at inlet
$\rho_{g}$	[kg/m³]	MDB	Gas density at inlet
$\rho_{s}$	[kg/m³]	MDB	Solids density at inlet
$a$	[m]		Height of blades channel in axial gas entry
$A_{con}$	[m²]		Lateral area of the conical part
$A_{con/2}$	[m²]		Lateral area of the top half of conical part
$A_{cyl}$	[m²]		Lateral area of the cylindrical part
$A_{e1}$	[m²]		Average wall area considered for the first revolution after entry
$A_{f}$	[m²]		Lateral area of vortex finder
$A_{sed}$	[m²]		Sedimentation area
$A_{sp}$	[m²]		Frictional area of the spiral in spiral gas entry
$A_{top}$	[m²]		Area of upper wall
$A_{tot}$	[m²]		Total wall friction area
$b_{e}$	[m]	UP/	Width of gas entry/blade channel
$d$	[m]	SP	Particle diameter
$d_{50}$	[m]	SP	Particle size median
$d_{b}$	[m]	UP	Thickness of blades in axial gas entry
$d_{exit}$	[m]	UP	Diameter of particles exit
$d_{f}$	[m]	UP	Diameter of vortex finder
$d_{o}$	[m]	UP	Outer diameter of cyclone
$d_{main,l}^{*}$	[m]		Cut size of separation on the first revolution due to exceeding the loading limit
$d_{main,v}^{*}$	[m]		Cut size of separation in internal vortex of main stream
$d_{sec,v}^{*}$	[m]		Cut size of separation at vortex finder in secondary stream
$D$	[-]	UP	Coefficient for grid efficiency curve calculation according to Muschelknautz
$h_{con}$	[m]		Height of the cone part of cyclone
$h_{con,eff}$	[m]		Effective height of the cone part of cyclone
$h_{cyl}$	[m]	UP	Height of the cylindrical part of cyclone
$h_{e}$	[m]	UP	Height of gas entry
$h_{f}$	[m]	UP	Height (depth) of vortex finder
$h_{sep}$	[m]		Height of separation zone
$h_{tot}$	[m]	UP	Total height of cyclone
$k$	[-]		Exponent for solids loading threshold in main stream
$K_{main}$	[-]	UP	Constant for solids loading threshold in main stream
${\dot{m}}_{in,g}$	[kg/s]	SP	Gas mass flow at inlet
${\dot{m}}_{in,s}$	[kg/s]	SP	Solids mass flow at inlet
${\dot{m}}_{out,s,s}$	[kg/s]		Solids mass flow at solids outlet
${\dot{m}}_{out,s,g}$	[kg/s]		Gas mass flow at solids outlet
${\dot{m}}_{out,g,s}$	[kg/s]		Solids mass flow at gas outlet
${\dot{m}}_{out,g,g}$	[kg/s]		Gas mass flow at gas outlet
$n$	[-]		Parameter for calculating secondary stream
$N_{b}$	[#]	UP	Number of blades in axial gas entry
${\overline{r}}_{con}$	[m]		Mean radius of the conical part
$r_{core}$	[m]	UP	Core radius of blades in axial gas entry
$r_{e}$	[m]		Radius of the middle gas streamline at gas entry
${\overline{r}}_{e}$	[m]		Mean radius of the gas streamline at gas entry
$r_{exit}$	[m]		Radius of the particles exit
$r_{exit,eff}$	[m]		Effective radius of the particles exit
$r_{f}$	[m]		Radius of vortex finder
$r_{o}$	[m]		Outer radius of cyclone
${\overline{r}}_{z}$	[m]		Reference mean radius
$R_{in}(d)$	[-]		Mass fraction of particles with size $d$ at inlet
$u_{con}$	[m/s]		Tangential velocity at mean cone radius
$u_{e}$	[m/s]		Tangential velocity at gas streamline radius at gas entry
$u_{f}$	[m/s]		Tangential velocity at vortex finder
$u_{o}$	[m/s]		Tangential velocity at outer cyclone radius
$v_{e}$	[m/s]		Inlet velocity in the middle gas streamline at gas entry
${\dot{V}}_{in,g}$	[m³/s]		Gas volume flow at inlet
${\dot{V}}_{\sec}$	[m³/s]		Gas volume flow of secondary stream
$w_{50}$	[m/s]		Sinking speed at which 50% of particles are sedimented at wall
$w_{split}$	[-]		Fraction of material going to main stream
${\overline{z}}_{e}$	[m²/s]		Mean centrifugal acceleration along streamline

UP: User-defined model parameters
MDB: Value from materials database
SP: Value from the input stream

Note

Model parameters:

Name	Symbol	Units	Description	Values
d_o	$d_{o}$	[m]	Outer diameter of cyclone	≥0.01
h_tot	$h_{tot}$	[m]	Total height of cyclone	≥0.01
h_cyl	$h_{cyl}$	[m]	Height of the cylindrical part of cyclone	≥0.01
d_f	$d_{f}$	[m]	Diameter of vortex finder	≥0.01
h_f	$h_{f}$	[m]	Height (depth) of vortex finder	≥0.01
d_exit	$d_{exit}$	[m]	Diameter of particle exit	≥0.01
Entry shape			Gas entry shape	Rectangular slot/Full spiral/Half spiral/Axial
b_e	$b_{e}$	[m]	Width of gas entry	≥0.01
h_e	$h_{e}$	[m]	Height of gas entry	≥0.01
epsilon	$\varepsilon$	[°]	Spiral angle in spiral gas entry	[0…360]
N_b	$N_{b}$	[#]	Number of blades in axial gas entry	≥1
d_b	$d_{b}$	[m]	Thickness of blades in axial gas entry	≥0
r_core	$r_{core}$	[m]	Core radius of blades in axial entry	≥0
Blade shape			Blades shapes in axial gas entry	Simple straight/Curved/Curved and twisted
delta	$\delta$	[°]	Angle of attack of blades in axial gas entry	[15…30]
lambda_0	$\lambda_{0}$	[-]	Wall friction coefficient of pure gas	≥0
D	$D$	[-]	Coefficient for grid efficiency curve calculation according to Muschelknautz	[2…4]
K_main	$K_{main}$	[-]	Constant for solids loading threshold in main stream	[0.02…0.03]
eta_adj	$\eta_{adj}$	[-]	Separation efficiency adjustment factor	[0…1]
Plot			Whether to generate plots	YES/NO