Granulator

This unit represents a simplified model of a fluidized bed granulation reactor. The model does not take into account attrition of particles inside the apparatus and does not keep properly any secondary distributed properties except size.

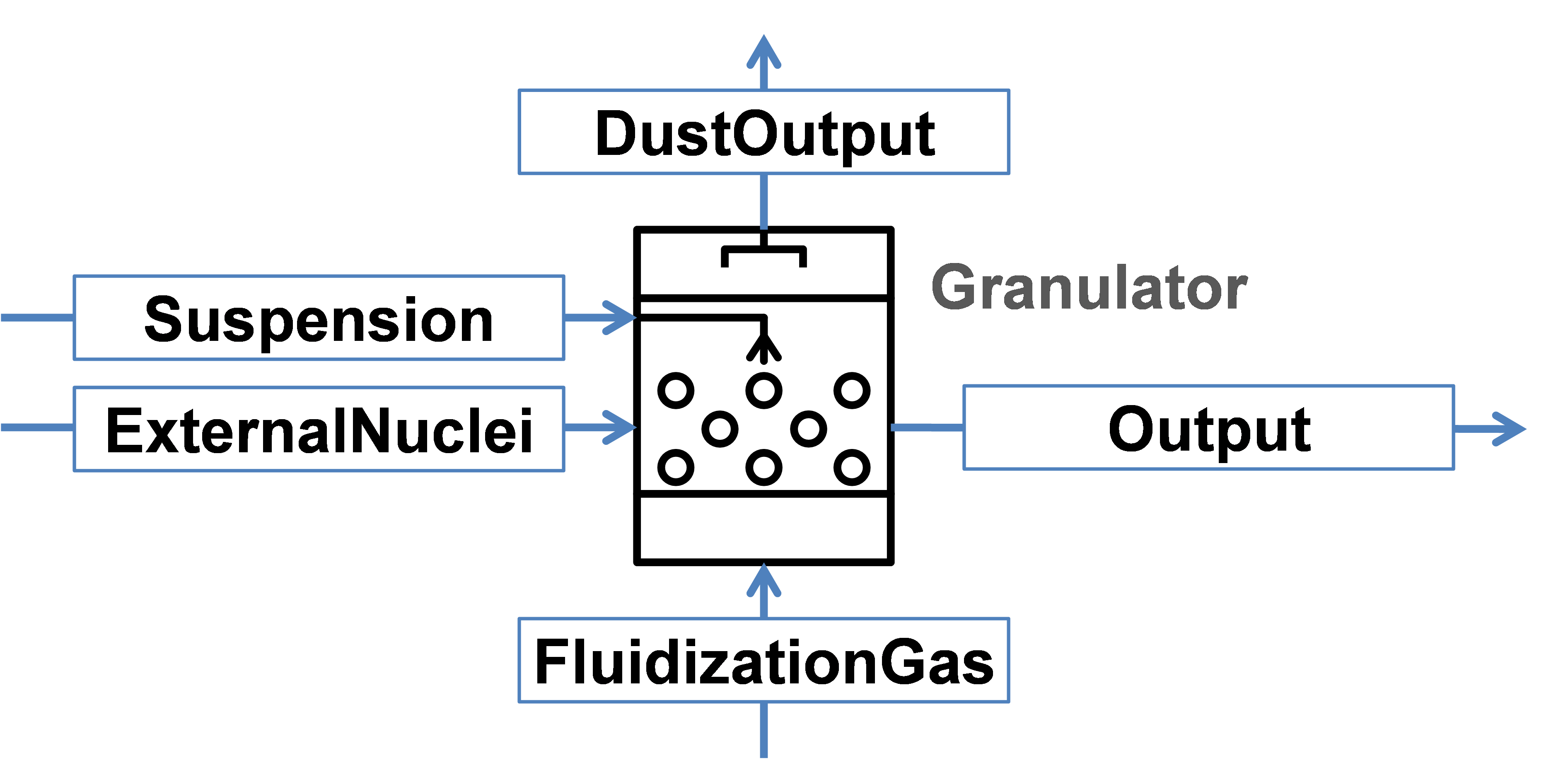
Continuous granulator

$\frac{dq_{3,i}}{dt} = -G_e\,\frac{q_{3,i} - q_{3,i-1}\,\left(\frac{d_{p,i}}{d_{p,i-1}}\right)^3}{\Delta d_i} + \frac{\dot{m}_{in}}{M_{tot}}\,q_{3,i}^{in} - \frac{\dot{m}_{out}}{M_{tot}}\,q_{3,i}$

$G_e = \frac{2\dot{m}_e}{\rho_{s,susp} \cdot A_{tot}}$

$A_{tot} = \frac{6M_{tot}}{\rho_s} \sum\limits_{i} \frac{q_{3,i}\cdot \Delta d_i}{d_{p,i}}$

$\dot{m}_e = \dot{m}_{s,susp}\,(1 - K_{os})$

$\dot{m}_{out} = \dot{m}_{in} + \dot{m}_{e}$

$\dot{m}_{in,liq} = (1 - K_{os}) \cdot \dot{m}_{sus,liq} + \dot{m}_{nuc,liq} + \dot{m}_{gas,liq}$

$\dot{m}_{gran,liq} = \begin{cases} u_{moist} \cdot \dot{m}_{out} & u_{moist} \cdot \dot{m}_{out} \leq \dot{m}_{in,liq} \\ \dot{m}_{in,liq} & u_{moist} \cdot \dot{m}_{out} > \dot{m}_{in,liq} \\ \end{cases}$

$\dot{m}_{dust} = \dot{m}_{s,susp}\cdot K_{os} + (\dot{m}_{susp} - \dot{m}_{s,susp} + \dot{m}_{fl,g} - \dot{m}_{gran,liq})$

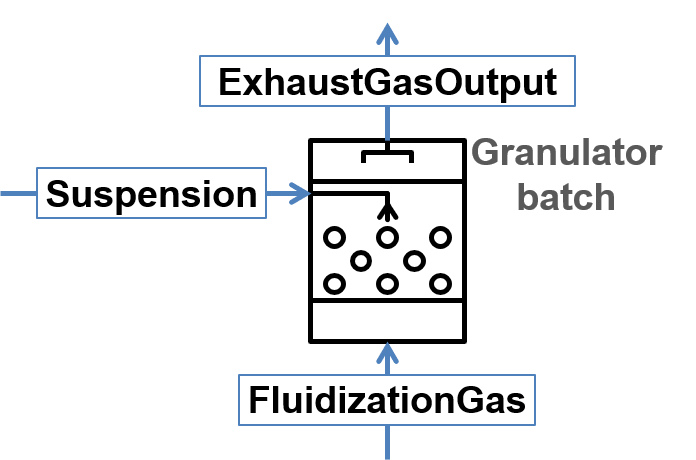
Batch granulator

$\frac{d(M_{tot}q_{3,i})}{dt} = -G_e\,\frac{M_{tot}q_{3,i} - M_{tot}q_{3,i-1}\,\left(\frac{d_{p,i}}{d_{p,i-1}}\right)^3}{\Delta d_i}$

$G_e = \frac{2\dot{m}_{s,susp}}{\rho_{s,susp} \cdot A_{tot}}$

$A_{tot} = \frac{6M_{tot}}{\rho_s} \sum\limits_{i} \frac{q_{3,i}\cdot \Delta d_i}{d_{p,i}}$

$\frac{dM_{tot}}{dt} = \dot{m}_{s,susp}$

$\dot{m}_{exh} = \dot{m}_{l,susp} + \dot{m}_{fl,gas}$

Note

Notations:

$q_3$ – mass density distribution of particles inside apparatus

$q_3^{in}$ – mass density distribution of external particles from ExternalNuclei stream

$\Delta d$ – class size

$d_p$ – particle diameter in a class

$\dot{m}_{in}$ – mass flow of input nuclei

$\dot{m}_{out}$ – output mass flow of the product

$\dot{m}_{dust}$ – output mass flow from the DustOutput

$\dot{m}_{susp}$ – total mass flow of the suspension

$\dot{m}_{s,susp}$ – mass flow of the solid phase in the Suspension inlet

$\dot{m}_{fl,g}$ – mass flow of the gas phase in the FluidizationGas inlet

$\dot{m}_{exh}$ – output mass flow from the ExhaustGasOutput

$\dot{m}_{e}$ – effective mass stream of the injected suspension

$\dot{m}_{gran,liq}$ – liquid mass flow leaving the granulator with granules

$\dot{m}_{in,liq}$ – total effective mass flow of liquid

$\dot{m}_{sus,liq}$ – mass flow of the liquid phase in the Suspension inlet

$\dot{m}_{nuc,liq}$ – mass flow of the liquid phase in the ExternalNuclei inlet

$\dot{m}_{gas,liq}$ – mass flow of the liquid phase in the FluidizationGas inlet

$M_{tot}$ – holdup mass

$u_{moist}$ – moisture content of granules (dry basis)

$\rho_{s,susp}$ – density of solids in the holdup

$G_{e}$ – effective growth rate

$A_{tot}$ – total surface of particles in the granulator

$K_{os}$ – overspray part in the suspension

Note

particle size distribution is required for the simulation. This unit is applied for solid, liquid and gas phases.

Note

Input parameters needed for the simulation:

Name	Symbol	Description	Units	Boundaries
Kos	$K_{os}$	Overspray part in the suspension	[–]	0 ≤ $K_{os}$ ≤ 1
Granules moisture content	$u_{moist}$	Moisture content of granules (dry basis)	[–]	0 ≤ $u_{moist}$
Relative tolerance	–	Relative tolerance for equation solver	[–]	0 < RTol ≤ 1
Absolute tolerance	–	Absolute tolerance for equation solver	[–]	0 < ATol ≤ 1

Note

State variables:

Name	Symbol	Description	Units
Atot	$A_{tot}$	Total surface of particles in the granulator	[ $m^2$ ]
Mtot	$M_{tot}$	Total mass of all particles in the granulator	[kg]
Mout	$\dot{m}_{out}$	Output mass flow of the product	[kg/s]
Mdust	$\dot{m}_{dust}$	Output mass flow of dust	[kg/s]
G	$G_{e}$	Effective growth rate	[m/s]
PSDi	$q_{3,i}$	Mass density distribution of particles	[1/m]